点到直线最短距离
问题描述:
对于三维空间中的直线方程
$p(t) = o + t\vec{d}$
其中$o$是原点, $\vec{d}$是单位方向向量。
对于给定的点$q$, 求出t的值, 使得直线上的点$p^\prime=p(t)$到$q$点的距离最近。
问题分析:
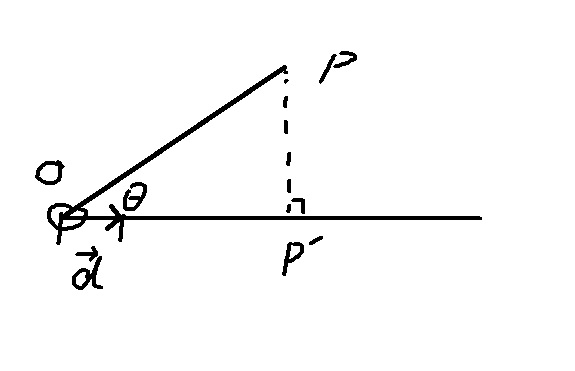
其实我们都知道点到直线垂线最短, 所以垂线与直线的交点即为所求:
如图, 因为$\vec{d}$为单位向量, 这里所求的t即为点$p^\prime$到射线原点$o$的距离, 也正是向量$q-o$在向量$\vec{d}$上的投影, 我们可用$\cos\theta|q-o|$表示($\theta$为$q-o$与$\vec{d}$的夹角)。
再次因为$\vec{d}$为单位向量,$|\vec{d}|=1$ 有:
$t=\cos\theta|q-o|=\cos\theta|q-o||\vec{d}|=(q-o)\cdot\vec{d}$
当d不为单位向量时, 还需要除去d向量的长度
$t=\cos\theta|q-o|=\frac{\cos\theta|q-o||\vec{d}|}{|\vec{d}|}=\frac{(q-o)\cdot\vec{d}}{|\vec{d}|}$
求出位置参数p后, 回代至对应的直线方程即可求出目标点$p^\prime=p(t)$
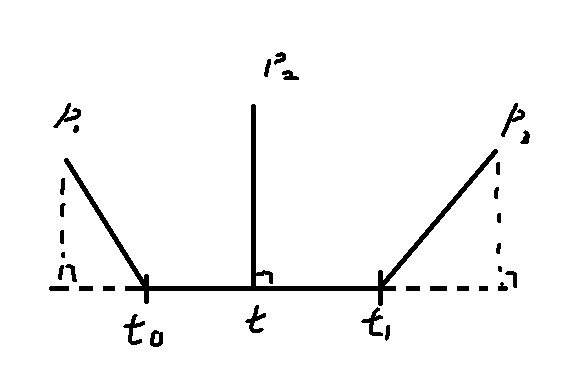
最后, 对于线段来说, 假设线段的起点为$t0$, 终点为$t1$。当求出的参数$t<t0$时, 则端点$t0$即为所求。当$t>t1$时, 则端点$t1$即为所求。
示例代码:
1 | |
reference:
3D Math Primer for Graphics and Game Development, 2nd Edition
我画的图好丑啊!TAT凑合着看吧